Convolutional (Faltung) Codes

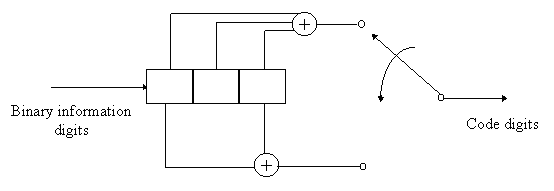
A simple rate ½ convolutional code encoder is shown below.
 

The rectangular box represents one element of a serial shift register.  The contents of the shift registers is shifted from left to right. The circle with a plus sign inside it represents XOR operation. Notice how the code digits which are output by the encoder are multiplexed into a serial stream of binary digits.   For every binary digit that enters the encoder, two code digits are output.   Hence code rate = 1/2.

In general, the code rate R_code = k / n

The constraint length K of a convolutional code is defined as the number of shifts over which a single message bit can influence the encoder output.

HOW TO DETERMINE THE OUTPUT CODEWORD ?

State Diagram Approach

• The corresponding state diagram for the rate 1/2, K = 3 convolutional code is shown below.  Notice that there are four states [00] , [01], [10], [11], corresponding to the (K-1)=2 binary digit tuple.

• We may assume the encoder starts in the all-zero state [00]

STATE TABLE

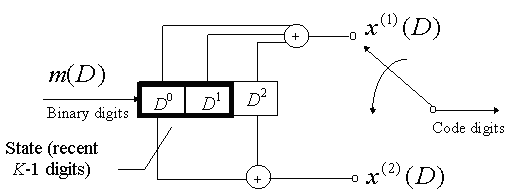
• Notice how all the combinations of the initial state and input digit are used to first determine the final state, and then the output codeword.

• Now we use this state table to draw the state diagram as shown below.

STATE DIAGRAM

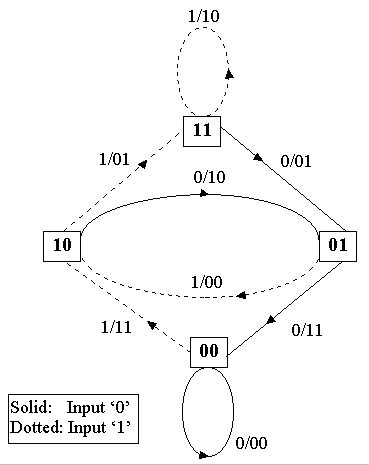
KEY

1/01 This means for example, that the input binary digit to the encoder was 1 and the corresponding codeword output is 01.

  This represents the state of the encoder.  In this example, the state is 01.

Copyright © Janak Sodha , 2000